Estimating fatalities
Now we will finally start comparing probable effects of a tactical nuclear strike to a bad nuclear meltdown. We will start with immediate deaths you could expect from each event. This is not much of a comparison: the answer is going to be “a tactical nuclear strike would entail far, far more deaths than a nuclear meltdown.” But let’s go through the comparison process nevertheless.
Estimating deaths for a nuclear bomb
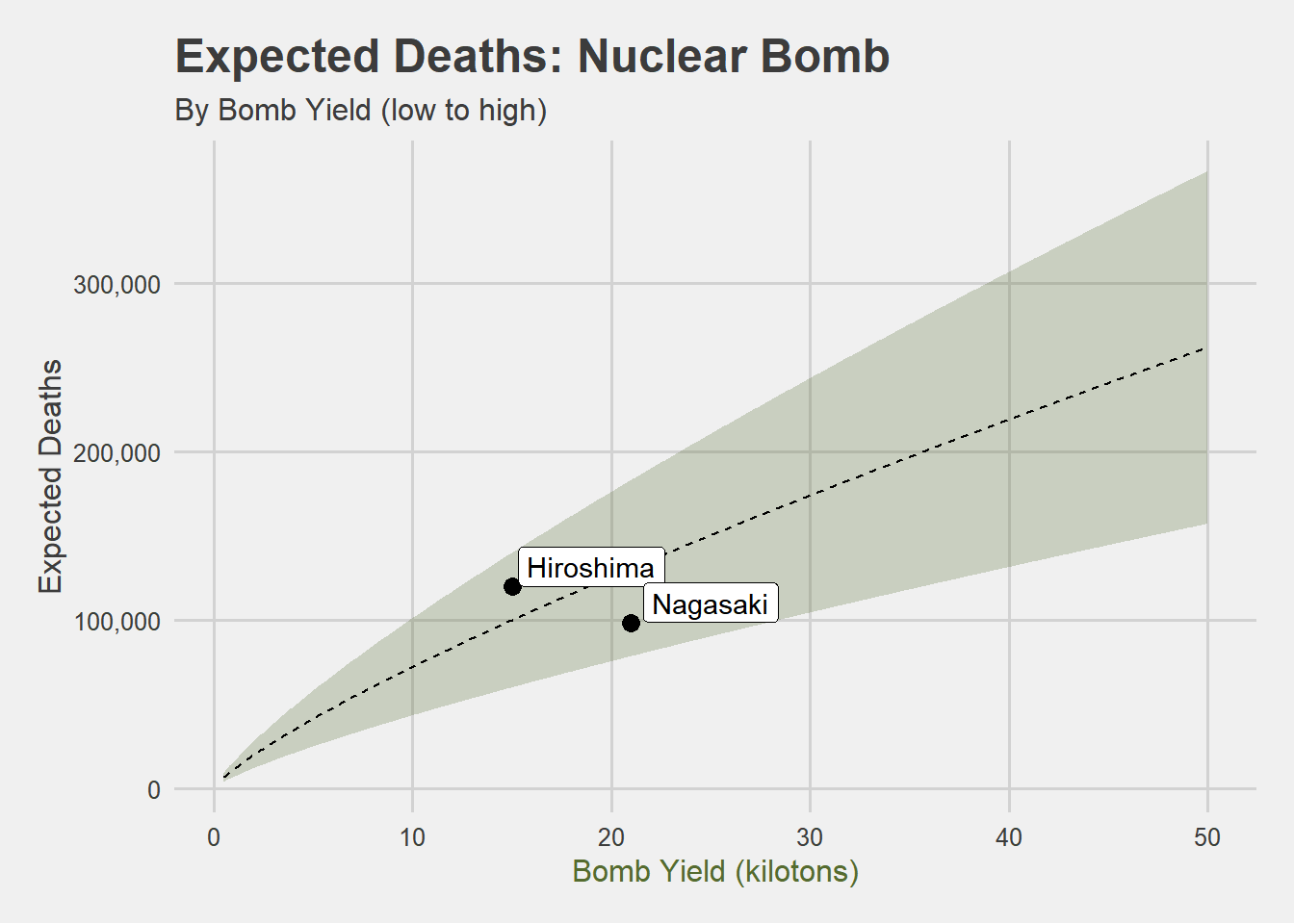
Estimating the deaths for a nuclear bomb is not an exact science, mostly because it depends on where the bomb is set off. Hiroshima, for example, saw considerably more casualties than did Nagasaki even though the bomb dropped on Hiroshima (“Little Boy”) was only 15 kilotons, compared to the 21 kiloton bomb (“Fat Man”) dropped on Nagasaki. And that primarily comes down to population–“Little Boy” hit an area of higher population density than did “Fat Man”.
It is, in fact, quite possible for Russia to choose a target to bomb that is largely symbolic and not full of very many people–a field somewhere, maybe, where nobody lives. The lower limit on the number of casualties is therefore completely within Russia’s control.
However, let’s assume a high-density target is picked for the purposes of this comparison. In this case, the expected deaths will mostly depend on the yield of the weapon. My method of estimating deaths-per-kiloton is as follows:
Assume the blast radius of the overall explosion is proportional to the blast radius of the fireball, and that the instantaneous casualty rate is proportional to both of those. Then we can use the formula from The Effects of Nuclear Weapons to calculate the size of the fireball from the yield of the bomb:
\[ Radius_{fireball} = 90 * Y^{0.4} \]
where Y is the bomb yield in kilotons. We can then convert to expected deaths by turning the radius into an area and multiplying be a constant that we tune so that it yields about the right casualties for the average between Hiroshima and Nagasaki (about 100,000 people). This turns out to be:
\[ Deaths = 0.451 * \pi*(90 * Y^{0.4})^2 \]
Then we can use the difference between Hiroshima and Nagasaki as a sort of a confidence interval and say that actual casualties will then be between +/- 15% of the values our equation gives. This is obviously just a very crude model, but with the uncertainties we’re dealing with, there’s not much point to making it more accurate.
I tested out my equation by comparing its results to the results of various online “nuclear blast simulators”, which let you pick locations and bomb yields and then get back the number of deaths and injuries that might be expected to result. One such simulator can by found here: NukeMap.
I found that for bombs ranging from 0.5 kilotons to around 50 kilotons, my estimation procedure was producing results very similar to the online nuclear blast simulators. However, the further I got beyond 50 kilotons, the less good the fit was and my equation started to predict a lot more deaths than the online simulators. I suspect that my equation is a drastic oversimplification of the actual mechanics of a nuclear explosion—but for anything under 50 kilotons, it appears to be a reasonable estimate. And it’s something I can graph–so I’m going with it.
Anything over 50 kilotons is also only questionably in the “tactical” category, anyway. Far more powerful nukes do exist, of course–Russia has bombs easily 20 times as powerful as that in its inventory. But we are considering here only the lower-energy case, on the assumption that Russia would try to get away with something less deadly first without provoking full civilization-ending levels of retaliation.
At any rate, if you graph the number of expected deaths by letting off a tactical-sized nuclear bomb in a populated area with these assumptions, you get something like this:
You can see that even within bombs that might be considered of “tactical” size, there is quite a wide variance in fatalities that might be expected, depending on the yield of the weapon. You have to zoom into the graph pretty tightly to see what sorts of casualties you might expect from the very smallest of tactical nukes (in the range of ~0.5 kilotons):
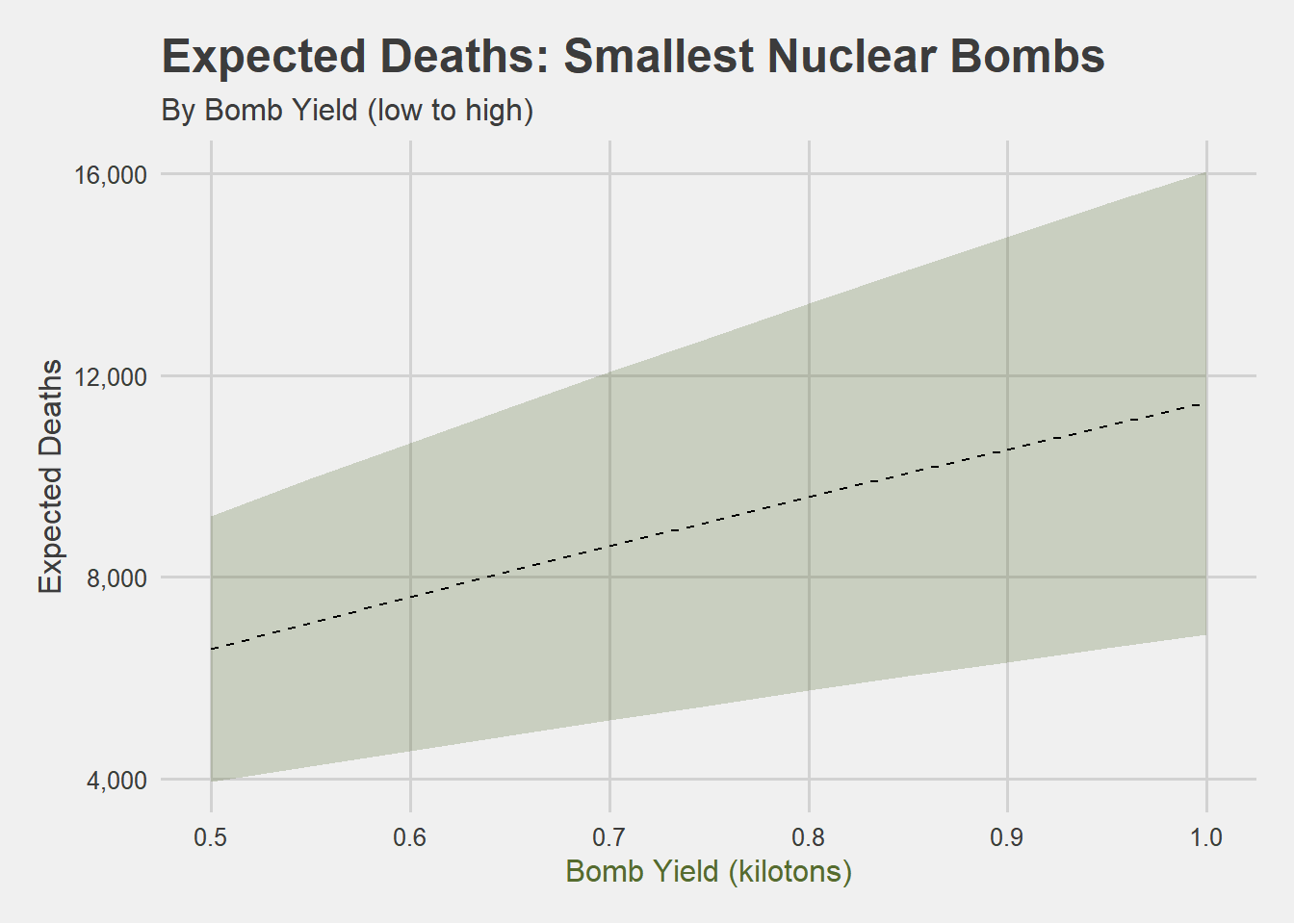
I have to admit that the best-case estimate for the smallest kinds of nuclear bombs is not as bad as I was expecting; 4,000 to 8,000 dead doesn’t sound as apocalyptic as the imagination typically evokes when you hear the phrase “nuclear bomb”. Note, however, that this amount is right around equal to the estimate for total civilian casualties of the war so far, as of the beginning of September. So, that’s seven months of war worth of people, killed in a matter of minutes with one bomb.
Estimating deaths for a nuclear meltdown
This estimate is harder to do, largely because we have only one historical example of people directly dying from a nuclear meltdown: Chernobyl. We have already discussed how it is difficult to see how the PWR reactors in Ukraine could fail in a way that would lead to the same types of death as happened at Chernobyl. So if we want to guess at how many people would die in some sort of PWR reactor accident, we are forced to imagine something that has never happened before.
For these reasons, I am going to assume that Chernobyl is almost the worst case scenario that we can reasonably expect might happen if the Russians were to try to create a nuclear meltdown that was as bad as they could make it. Arbitrarily, I’m going to say that maybe an accident 25% worse than Chernobyl could be engineered, but no worse. Also arbitrarily, I’m going to say that the deaths you could expect will go in some linear scale from zero up to this arbitrary somewhat-worse-than-Chernobyl scenario.
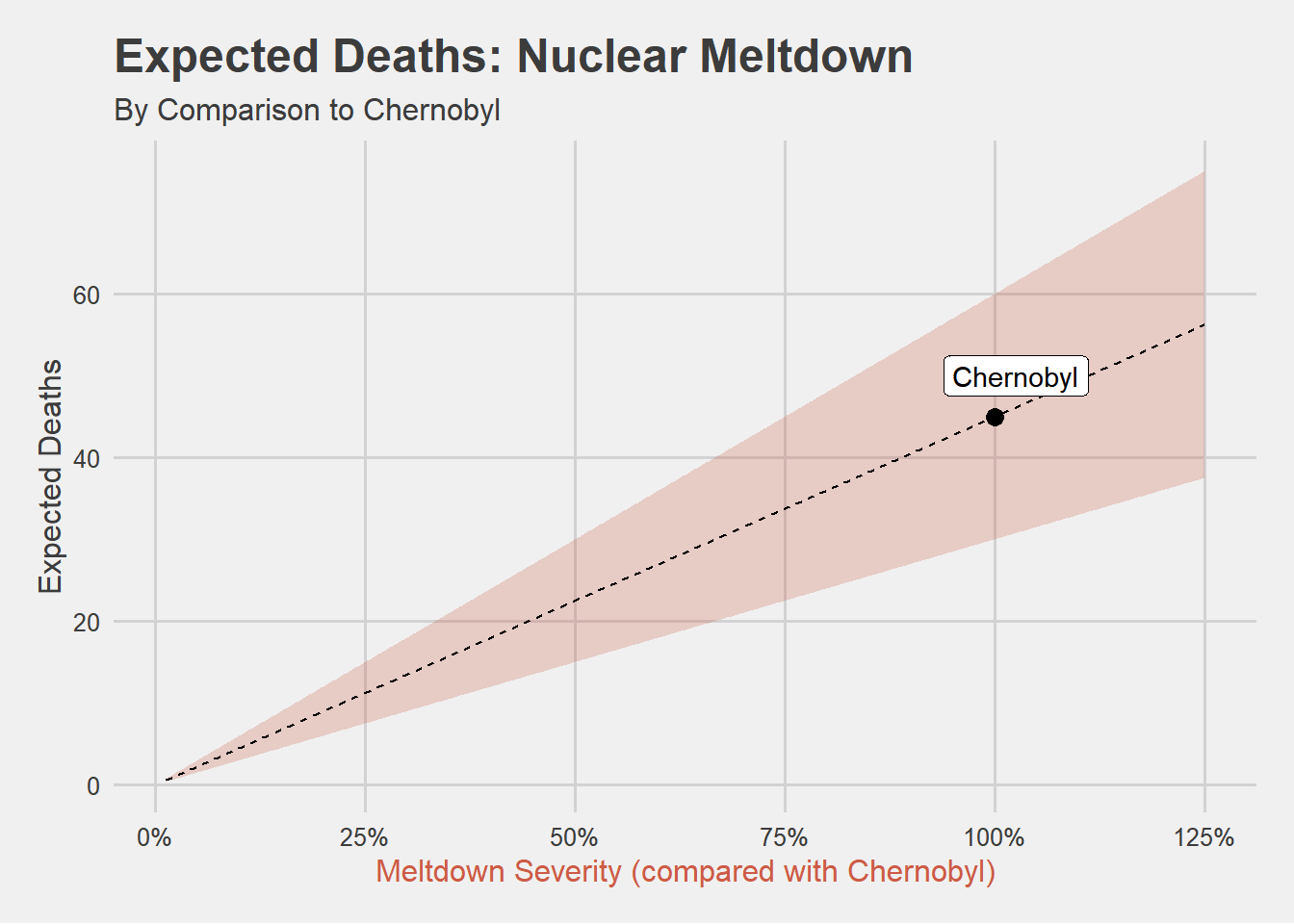
So, how many people did die at Chernobyl, initially? The current official count stands at 31: all of them plant workers and firefighters. However, given that the U.S.S.R. was an endless font of lies and misinformation, can we trust this number? I think the answer is mostly, “yes”. The original number reported by the government was first zero, and then 2. The number 31 came a lot later, after investigation involving international authorities.
Furthermore, after the U.S.S.R. fell, there was a period of relative openness during which a lot of old Soviet secrets came out. From this period, we know about thousands of people who claimed long-term effects from the radiation of Chernobyl and were trying to get compensated by the government. I reason that if we have heard about these thousands of people, then we also would have heard about most other family members who were trying to get compensated for loved ones who died fighting the fires, if they existed.
I am going to accept 31 as a minimal number of people who died in the initial days at Chernobyl, and arbitrarily say that it could have been up to twice that number of people, really. This, then, will be the benchmark by which we will guess at how many fatalities we could expect from other nuclear meltdowns.
With these assumptions, if you graphed deaths you would expect given how bad in comparison to Chernobyl a hypothetical nuclear meltdown was–you would get a graph like this:
Absurdity of this comparison
This was an excessive amount of calculation to state the obvious: the immediate fatalities you would expect from a nuclear meltdown are not at all similar to the number of deaths even the smallest of tactical nukes could cause. They are really not comparable at all. I can drive this point home visually by trying to plot these two results on the same graph
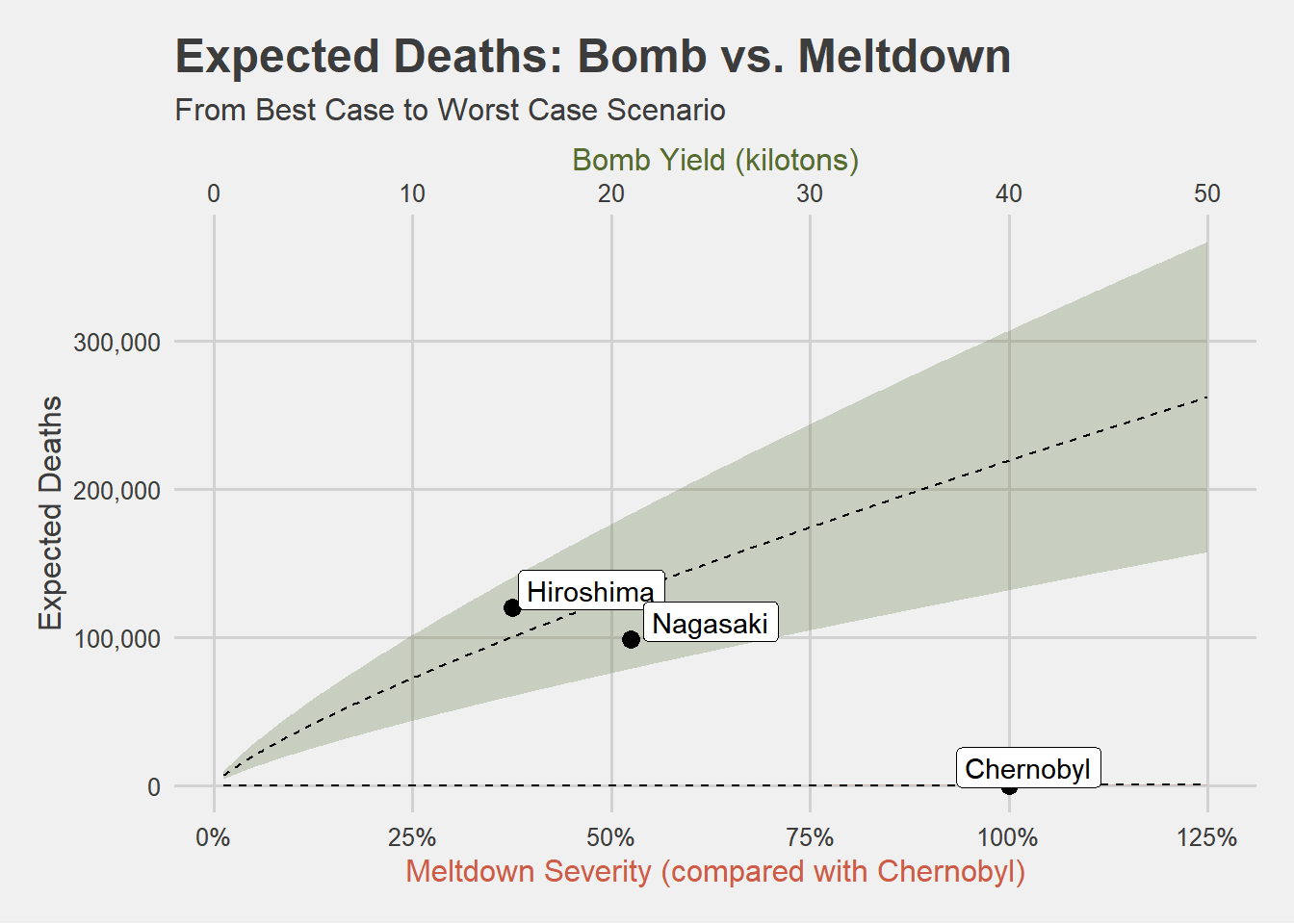
Given to the range of realistic death tolls you would expect to see from mildly powerful nuclear weapons, the deaths you would expect from a nuclear meltdown are effectively zero–a rounding error–in comparison.
Conclusion
In terms of immediate fatalities, there is no reasonable comparison between a nuclear meltdown and a nuclear bomb, no matter how bad you could imagine the meltdown to be and no matter how small you posit the nuclear bomb. These are events of categorically different magnitudes. The fact that both contain the word “nuclear” probably tricks a lot of people into categorizing them similarly, but at least in terms of immediate casualties, they should not.